What's Up With Evolutionary Dynamics?!

This post is going to introduce some stuff from the incredible field of evolutionary dynamics. Evo-dynamics is about applying game theory to biology and evolution via mathematically models. It's been used to explain things like cooperation in biology and even concepts like altruism. We'll start off by looking at the Prisoner's Dilemma:

The Prisoner's Dilemma (PD) shows up in both game theory and evolutionary dynamics as a game which motivates the questions of 'when is cooperation a good idea' and 'why is cooperation sometimes selected for'. The idea is that you have two separated prisoners involved in the same crime who are each given two choices:

1) confess to the crime, thus defecting against your friend
2) keep your mouth shut, thus cooperating with your friend

There are three possible outcomes:

1) if both prisoners cooperate (stay quiet), they both get a year in prison
2) if both prisoners defect (confess), they both get 7 years in prison
3) if one prisoner cooperates whilst the other defects, the cooperative prisoner gets 10 years and the defector gets no years

This can be described in payoff-matrix form where the row = your choice and the column = their choice:

So which choice is rational?

Let's say they cooperate (remain silent). If you defect you go free, whereas if you cooperated you'd get a year in prison
Let's say they defect. If you defect you only get 7 years in prison, whereas if you cooperated you'd get 10.

No matter what the other prisoner chooses, it is rational for you to defect in order to minimise your sentence. When there is a set of strategies that can be played with no player having any good reason to switch strategies, it's called a Nash Equilibrium. So in this case, defect-defect is a Nash Equilibrium because either player could only do worse by switching to cooperation.

What would happen if we applied a similar game to a population whose fitness is dependent on how the outcome of the game.

So each individual in our population is hardwired to either cooperate or defect every time they come across another individual. Let's handle some terminology: we've got an infinite population so we can describe the abundance of one 'species' (strategy) as a frequency from [0,1]. By the way when I say species, it could be referring to two members of the same species with different strategies. In this example we'll say x is the frequency of C (cooperators) and 1-x is the frequency of D (defectors).

The fitness of a species is an indication of how fast its frequency increases, and it's given by:

which reads 'for a species 'i', the fitness of 'i' is the sum of its payoffs against every species (including itself) multiplied by the frequency of that species' so the vector x is the set of the species, 'a' is the payoff matrix and x_j is the frequency of a given species. So to calculate it for our species C and D, the fitness of C is 3*(x) + 0*(1-x) = 3x = 3x and the fitness of D is 5*(x) + 1*(1-x) = 4x + 1. How do these fitnesses affect reproduction (i.e. changes in frequency)? We can answer that with the replicator equation:

which can be read as 'the rate at which a species frequency changes with respect to time is given by that species frequency times the difference between its fitness and the average fitness across all species'. So phi(x) represents the average fitness. This is intuitive due to the species increasing its frequency if it has an above-average fitness. So if the fitness of a species is equal to the average, its frequency won't change, and if its fitness is greater than the average, its frequency will rise, and otherwise it will fall.

Considering the replicator equation we can see what happens when we have a population of C's and D's. If we start with a 50/50 split in the population, the average fitness is 3x/2 + (4x+1)/2 = (7x+1)/2. Clearly the D's have a fitness above the average so they will be increasing their frequency and the C's will thus tend to a frequency of 0. At that point, when x = 0, the population will be in equilibrium with the replication rates all being 0 (because there's no more C's). BUT what if we started off with x = 1 i.e. there are no D's? This means now the average fitness is just the fitness of C's which is 3x and so the population won't change meaning this is another equilibrium point. The difference between the two equilibrium points is that the first is a 'stable' equilibrium, meaning small deviations from it will be corrected as the system naturally tends back towards the equilibrium point, whereas the second is not a stable equilibrium, as for example if you were to add a minuscule amount of D's to the mix, their superior strategy against cooperators would have them easily invade the population and move the frequency of C's down from 1.

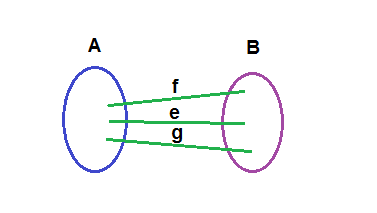
The things I'm describing here can be represented by a simplex which is the set of all points which describe the frequencies of each species in a population. If we were only considering a population of one species, the simplex would be 0-dimensional i.e. it would be a single point. Because we're dealing with two species, we have a line:

The right of the simplex represents when x = 1 (i.e. there are only C's) and the left represents when x = 0 (i.e. there are only D's). a closed circle represents a stable equilibrium and an open circle represents an unstable equilibrium. The arrow says that if you lie on the arrow then the frequency of C's moves in that direction (in this case, towards 0).

Considering the only thing which effects this simplex is the payoff matrix, let's take a payoff matrix with payoffs a,b,c and d and see what kind of simplex we get depending on their relative values, with the species A and B (this time x = frequency of A's):

To recap on what this means, if two A's meet then they'll both get a payoff of a. If an A meets a B, it gets a payoff of b. If a B meets an A it gets a payoff of C and if two B's meet they both get a payoff of d. The fitness of A and B is their average payoff.

So the fitness of A = ax + b(1-x) and the fitness of B = cx + d(1-x)

the average fitness is:
 x(ax + b(1 - x)) + (1 - x)(cx + d(1 - x))

and the replicator equation for A is:
x((ax+b(1-x))-x(ax + b(1 - x)) + (1 - x)(cx + d(1 - x)))
= -x(x-1)(x(a - b + c - d) + b + d)

And yes, I used a calculator for that.

We can now consider what happens for various relative values of a,b,c and d.

So let's say a > c and b > d. This means that no matter what A will dominate over B because it always gets a higher payoff and thus has a higher fitness than average while there's still B's floating around.

If it's the other way around and a < c and b < d then B will dominate over A.

If a > c but b < d then we can consider three situations:
1) there aren't many A's to start with so despite A's getting a better payoff against other A's than B's, there aren't enough A's for that to make a difference as the majority of games will occur between A's and B's in which case the B's destroy the A's, meaning the A's go extinct.
2) there aren't many B's to start off with, and the exact same logic applies: the B's will go extinct
3) there is a sweet spot where there are just enough A's and just enough B's for them to be in equilibrium, albeit an unstable one. To work out where this is you can solve A's replicator equation for when the rate of its changing frequency is 0 and you end up with x = (d-b)(a-b-c+d).

if a < c and b > d then each species gets a better payoff when interacting with the other species than interacting with their own species. This means we get a trend towards the middle of the simplex at a stable equilibrium. The position of that equilibrium is x = (d-b)/(a-b-c+d). The multiplication from above becomes a division, WHAT A TIME TO BE ALIVE (that's not sarcasm).

Finally, if a = c and b = d then it's impossible for selection to discriminate against either species because they are identical in their payoffs. This would give you a neutral simplex where no frequencies change but this is actually not accurate in terms of finite populations as neutral drift is enough to eventually wipe out one or the other species.

Here's a pictorial representation:

So we've looked at populations with two species. Before we go into more depth in the prisoners dilemma, let's consider what the implications of having three species are. As 1 species in a population gives us a 0D simplex i.e. a point, and then we get a line, now we get a triangle (the next step would be a triangular pyramid and then the dimensions go beyond what can easily be visualised). Let's consider the game of scissors paper rock (S,P and R) which has the quality that S dominates P, P dominates R and R dominates S. Here's the payoff matrix A:

What would happen if we had all three frequencies initialised to 1/3? There's no good reason why any of them would win over any others (i.e. their fitnesses will all be equal) so that is an equilibrium point. Is it a stable one? It turns out to be a neutral equilibrium point surrounded by neutral oscillations which go back to the edges but never touch them. This means if we had x_S (frequency of S) = 1/5 and x_P = 1/5 and x_R = 2/5, we'd see the point on the simplex orbit around the equilibrium point, passing the points (1/5,2/5,1/5) and (2/5,1/5,1/5). If we generalised the payoff matrix to be:

Then we can work out what the simplex will look like. If the determinant is =0 then we have the neutral oscillation situations from the traditional SPR game. If it's <0 then we've still got the interior equilibrium point (whether it's actually in the centre depends on the matrix) but it's unstable and all other points spiral out towards the edges asymptotically so the boundary of the simplex is an attractor (called the heteroclinic cycle). If the determinant is >0 then we have the spiral but this this time the interior equilibrium point is the attractor (so it's stable).

Note that although the oscillations can get asymptotically close to the edges, a rounding error can make a species completely extinct and then you'll end up with the remaining dominating species taking over completely. Not to mention that in finite populations there are no asymptotic protections against a species going extinct.

Now that we have some intuition behind how a population works with three species, let's go back to the prisoners dilemma. The two strategies we had were Defect and Cooperate, but these alone don't tell us much about how species behave. What would be more accurate is if two individuals interacting with eachother played the game on average m times. Now the number of strategies really open up. The multi-game analogue of the single-game defect strategy would be the always-defect strategy (ALLD). Likewise we have the always-cooperate strategy (ALLC). The third strategy we're going to look at it tit-for-tat (TFT). In TFT, your first move is to cooperate and after that you just do what your opponent did in the previous round. This time we're going to use a generalised payoff matrix for a single round with the variables T,R,P and S where T>R>P>S. You can remember them as Temptation to defect, Reward for cooperating, Punishment for mutual defection and Sucker's payoff for being the one who cooperates when the opponent defects.

Let's consider how these strategies to eachother:

ALLD vs ALLC: ALLD wins because in each round it gets the highest payoff T, and ALLC gets the lowest payoff S.

ALLC vs TFT: both get the R payoff, which is a big step-up for ALLC but neither strategy walks away with as much of a payoff as ALLD when it's up against ALLC

ALLD vs TFT: TFT starts off cooperating and gets the Sucker's payoff whilst ALLD gets the Temptation payoff but after that TFT just defects for the rest of the m-1 round so TFT walks away with S + P(m-1) and ALLD walks away with a slightly higher payoff T + P(m-1).

ALLC vs ALLC: both get a pretty good R payoff each round.

TFT vs TFT: same as above

ALLD vs ALLD: measly payoff of P each round.

We can make this more interesting (and more accurate) by giving TFT a complexity cost 'c' which is subtracted from its total payoff in each iteration. This means ALLC will now beat it and ALLC-ALLC interactions yield higher payoffs than TFT-TFT interactions.

as you can see, ALLD always wins against its opponent. HOWEVER, two ALLDs versing each other get a far lower payoff than interactions between TFTs and ALLCs. What does this mean? If we start with (1/3,1/3,1/3) frequencies then ALLD is going to dominate but as its frequency increases, its fitness decreases because there are less TFTs and ALLCs to fight. Meanwhile the TFTs fitness increases because TFT is only slightly outplayed by ALLD but gets high payoffs with all other interactions. So we'll see a growth of TFT and a shrink of ALLD. But now with less ALLDs floating around, ALLC can once again rise as it fairs better than TFT in a population low in ALLDs. But then we get back to the beginning where ALLDs can exploit the high numbers of ALLCs.

So we know we're going to get oscillations, but will they be neutral or inward/outward spirals? If we follow the convention of saying T = 5, R = 3,P = 1, and S = 0.1, m = 10 and c = 0.8, then we get a matrix like this:

I've looked all over for a picture of a simplex demonstrating this payoff matrix under the replicator equation but I can't find one. However, Imhof, Fudenberg and Nowak's 2005 study on the prisoner's dilemma has some simplexes under the replicator-mutator equation, which assigns a value u to rate at which one species mutates to another (I'm assuming there's an equal chance of mutating from one species to another proportional to fitness). Here's the replicator-mutator equation:

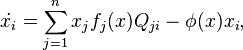
where Q is the matrix describing the probabilities of species j mutating to species i.

And here's some simplexes under this equation:

As you can see, this alone produces some crazy stuff. With very low mutation (u = 10^-8) we converge to the conventional replicator equation, and we can see that ALLD wins out in the end. Obviously with more mutation, the selection isn't as cut-throat so we see with u=10^-2 that there is a convergence to a stable equilibrium which has a high frequency of TFT. This is an interesting change which comes about through merely increasing the rate of mutation. Nonetheless the deterministic approach to the repeated prisoners dilemma overwhelmingly favours ALLD, which is intuitive due to ALLD-ALLD being the only nash equilibrium in the game. But is this what we see in finite populations?

The answer is no. In finite populations what we see is oscillations which have a time-average near the TFT vertex (i.e. most of the time is spent around there). Why is this the case? Good question. Finding out requires an understanding of how evolutionary dynamics works with finite populations, which has a whole lot of different processes (e.g. the Moran Process) and stochastic equations, but as this post has gotten long enough I'll leave you with the cliffhanger that finite populations and infinite populations can give us drastically differing results when simulating the same game.

Special thanks to Martin Nowak whose textbook on evolutionary dynamics provided a few of the images in this post a lot of insight into how evo-dynamics works.

What's Up With Signed Integers?!

In an earlier post we talked about how binary numbers worked (in fact we talked about how all bases work) for positive numbers with both integer and fractional parts. In this post we're going to talk about how negative integers are represented in binary.

Under status quo, let's say we have a computer which, due to a lack of foresight into memory allocation requirements, only holds 4 bits of memory. If we were to consider those bits to represent an unsigned number, here's what we would interpret the states as:

0000 = 0    0001 = 1    0010 = 2    0011 = 3
0100 = 4    0101 = 5    0110 = 6    0111 = 7
1000 = 8    1001 = 9    1010 = 10   1011 = 11
1100 = 12   1101 = 13   1110 = 14   1111 = 15

0,1,2,3,4,5,6,7,8,9,10,11,12,12,14,15

so we have 16 numbers, 0-15, so no surprises so far.

If we wanted to have as many negative numbers represented by our 4 bits as positive numbers, then we're going to end up with half as many positive numbers that we can represent. One possible way of going about this (which was my first impression) would be to reserve one bit for the sign of the number. Let's say we take the left-most (most significant) bit and say that if it's 0, we're dealing with a positive number and if it's a 1 we're dealing with a negative number. How will our representations change?

0000 =  0   0001 =  1   0010 =  2   0011 =  3
0100 =  4   0101 =  5   0110 =  6   0111 =  7
1000 = -0   1001 = -1   1010 = -2   1011 = -3
1100 = -4   1101 = -5   1110 = -6   1111 = -7

0,1,2,3,4,5,6,7,-0,-1,-2,-3,-4,-5,-6,-7

Not bad but a few problems arise:

Firstly we have two ways of representing 0. Not only is this a waste of a state (namely the binary number 1000) but computers very very often need to compare numbers to 0 so if there are two ways to represent 0 in binary then every time a computer wants to check whether a number is 0, it will need to check if it's +0 or -0 and the extra comparison is costly when we're dealing with processors that can do these kinds of things millions of times in a second.

Secondly, in terms of arithmetic, the computer needs to read the sign bit of both numbers if it wants to work out whether it needs to perform addition or subtraction on them.

Thirdly, it would be nice to have the numbers be in order like -7,-6,-5...0,1,2,3...6,7 so if you're incrementing or decrementing the number you don't need to worry about shifting gears when you get to 0.

Before I introduce the next method for representing signed integers, it's a good time to mention that these quarrels I have with the above method (called the sign-and-magnitude method) are not necessarily going to be solved by some super-method, and the method that computers actually use today (which will be later on in the post) was and still is subject to a lot of heated debate in light of the other methods.

The next method which is intuitive to me is the 'Excess K' method where you take your regular unsigned numbers and just give them an offset of K. For example we could choose K to be 8 meaning that each of our numbers will be translated 8 units to the left:

0000 = -8    0001 = -7    0010 = -6    0011 = -5
0100 = -4    0101 = -3    0110 = -2    0111 = -1
1000 =  0    1001 =  1    1010 =  2    1011 =  3
1100 =  4    1101 =  5    1110 =  6    1111 =  7

-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7

Note that you could have chosen your K to be 7 and you'd have a range of -7-8 which is just as valid.

Well we fixed quarrel #3 with the sign-and-magnitude method, an increase/decrease of 1 in the binary representation corresponds to an increase/decrease of 1 in the signed number itself. We also now only have a single 0. The only problem here, and it is a big problem, is arithmetic. If you want to add 1 and -5 then you're dealing with 1001 and 0011. This means you're dealing with (1+8) + (-5 + 8) = 12 and then you need to cancel out the excess 8's by subtracting 2*8 which gives you -4 (at least it gives the correct answer). Well actually if you used that process you'd then need to add another 8 afterwards to give -4 its binary representation so we may as well only ever subtract off one 8 instead of 2*8 after we do additions.

The other methods are the complement methods. What is a complement? Its easier to think about in terms of decimals:

For base 10 we can look at the 10's complement or the 9's complement of any number. If I have the number 531, the 10's complement of that is simply 1000 - 531 = 469. Why would we ever want to use this? Let's say I want to subtract 531 from 812. I suck at subtraction so it would be easier to just add 812 to -531 which by the above equation is (469 - 1000) i.e. add 469 and 812, and then subtract off 1000 when I'm done to get the answer to the question of what 812 - 531 is. 469 + 812 = 1281 meaning our answer is 1281-1000 = 281. To generalise, the 10's complement of a number n with d digits is 10^d - n (but if n=0 the complement is 0 which is reasonable when you consider that the number of digits is irrelevant to representing 0). 10's complements are good because removing the 10^d from the result of the addition at the end is easy, although actually calculating the complement in the first place isn't as easy as it could be. What you could do is instead of subtract n from 1000 you could subtract it from 999 (meaning you can do the subtraction digit by digit) and then add 1 at the end i.e. you're subtracting the rightmost digit from 10 and every other digit from 9 (which is just another way of subtracting n from 1000 because 1000 = 999 + 1).

So our 10's complement is 10^d - n and the way we implemented it actually utilised the 9's complement i.e. (10^d - 1 - n). So if I wanted the 9's complement of 531 that's just 999 - 531 = 468 (the 10's complement is 469 because 999 and 1000 differ by 1).

So there's 9's and 10's complements, and you may be wondering why we can't have an 8's complement or a 7's complement when dealing with decimal numbers. The answer is that if you did, and you wanted to subtract your number from say 8888, then if one of the digits is a 9 you'll need to take the subtraction beyond the current digit which defeats the purpose of having a complement.

Anyway now that we know what a complement is we can apply the concept to binary numbers. We shall start off with the 1's complement.

If we have a number 0010 (2) then the one's complement of it is 1111 - 0010 = 1101. The bits just get inverted. The formula for the 1's complement is 2^d - 1 - n. The 2's complement (the only other possible complement) is 2^d - n. so the 2's complement of 0010 is 10000 - 0010 = 1110. Just like how you could consider the 10's complement as the 9's complement plus 1, the 2's complement is the 1's complement plus 1. So the 2's complement of 0010 could be calculated as 1111 - 0010 + 1 = 1101 + 1 = 1110. Notice what happens when you add the 1 at the end: if the leftmost digit is a 0 (meaning it was a 1 before the inversion happened) then it becomes a 1 (i.e. the inverted digit is inverted again meaning it goes back to how it was in n originally). If the leftmost digit is a 1 then it becomes a 0 and the 1 gets carried all the way until there's a 0 to hold it. For example if you say n is 0101011000 then when calculating the 2's complement you first invert the digits so we get 1010100111 then you add one so we get 101010[1000]. The digits in the brackets are exactly what they were when we started so now we know that the easiest way to get the 2's complement is to just start from right to left and we ignore all the zeros and the first 1 that we see and then we start inverting the digits to the end.

Before I get into how this helps represent negative numbers in binary, notice that the complement of a complement is the original number. For example if we start with n and take the 2's complement we get (2^d - n) and if we take the 2's complement of that we get 2^d - (2^d - n) = 2^d - 2^d + n = n.

So how does this translate into representing negative numbers? Say I only allowed myself to represent decimal numbers with 3 digits. Clearly I need to halve my range of positive values in order to have equal representation of positive and negative numbers. We can say that 000 to 499 are positive and anything past that is negative and you just take the 10's complement to find out it's magnitude. e.g. 500 becomes -(1000 - 500) = -500, and 999 becomes -(1000 - 999) = -1. So we get a range of 0 to 499 in positive numbers and -1 to -500 in negative numbers.

In 9's complement we again say 000 to 499 just remain unchanged and represent positive numbers. Then everything else represents the negative of the 9's complement so 500 becomes -(999 - 500) = -499, and 999 becomes -(999 - 999) = -0. So we can represent 0 to 499 in positive numbers and -0 to -499 in negative numbers.

In 2's complement let's say again we can only store 4 bits, so 0000 (0) to 0111 (7) remain unchanged and 1000 (8) to 1111 (15) represent the negative of their 2's complements so with the table we used above:

0000 =  0   0001 =  1   0010 =  2   0011 =  3
0100 =  4   0101 =  5   0110 =  6   0111 =  7
1000 = -8   1001 = -7   1010 = -6   1011 = -5
1100 = -4   1101 = -3   1110 = -2   1111 = -1

Notice that you can easily tell when a number is negative because the leftmost digit is 1.

In 2's complement the 0000 (0) to 0111 (7) remain unchanged but the 1000 (8) to 1111 (15) represent the negative of their 1's complement:

0000 =  0   0001 =  1   0010 =  2   0011 =  3
0100 =  4   0101 =  5   0110 =  6   0111 =  7
1000 = -7   1001 = -6   1010 = -5   1011 = -4
1100 = -3   1101 = -2   1110 = -1   1111 = -0

Considering subtraction can be seen as adding a number and another number's complement i.e. A - B = A + (-B). Here's how a decimal computer would go about subtracting 531 from 712 using 10's complement:

531 --> 1000 - 531 = 469

712 + 469 = 1181

because we end up with an extra digit, remove the rightmost 1 because that represents the 1000 we added on at the beginning

1181 --> 181 and that's our answer.

If we ended up with a three-digit number then we can't just take off the rightmost 1 to subtract off 1000 so instead we take the complement of the number and store that e.g. 280 - 435:

435 --> 1000 - 435 = 575

280 + 575 = 855

855 is the 10's complement representation of the actual answer -145 because we are in excess of 1000 so if we wanted to print the answer we'd just go 855 - 1000 = -(1000 - 855) = -(10's complement of 855) = -145 i.e. take the 10's complement of 855 and stick a minus sign infront of it.

With 9's complement the process is exactly the same except if you get an extra digit holding a 1 (an end-carry) you need to do an end-around-carry. For example let's 712 - 531 using 9's complement:

531 --> 999 - 531 = 468

712 + 468 = 1180

you've got an end-carry but you can't just remove it because that would be removing 1000 when you want to remove 999 to get the true answer, so instead remove the rightmost digit and then add 1 i.e. 1000 = 999 + 1:

1180 --> 180 --> 181. Which is the same as we got with 2's complement.

If you're doing 9's complement subtraction with 280 - 435:

435 --> 999 - 435 = 564

280 + 564 = 844 which is correct in terms of 9's complement representations of negative numbers but if you want to print the actual result you'd go 999 - 844 is 155 so the answer is -155 (you've just taken the 9's complement again).

A question that just popped up in my head is 'what happens if you do the subtraction and end up with 999, because you won't have the extra digit telling you to subtract off 999 to get 0', but then I remembered that 999 = -0 so that a self-solving problem.

As for 2's complement subtraction it's very similar: if we wanted to subtract 10010 (26) from 11010 (18) then we follow the same process:

11010 --> 100000 - 11010 = 00110

10010 + 00110 = 11000 and considering there's no 6th digit we're dealing with a negative number so we can store it like that and if we want to print out what it we can take the negative of the 2's complement and say it's -(100000 - 11000) = -01000 = -8.

If we wanted to subtract 18 from 26 we'd end up with an extra 1 digit in which case we could just throw that away (i.e. take the negative of the complement again) to get our answer.

For 1's complement subtraction let's see what subtracting 26 from 18 is like:

11010 --> 11111 - 11010 = 00101

10010 + 00101 = 10111 which is negative and to find out the value we take the negative of the complement to give us -01000 = -8. If we had done 26 - 18 we'd have an end-carry so we'd need to discard that digit and add 1 because 100000 = 11111 + 1 so subtracting 100000 and then adding 1 is the same as subtracting 11111 i.e. taking the negative of the complement.

So the general process is to calculate A - B we take B's complement and then calculate A + (B's complement) and then take the negative of the complement of the result to get the true answer which, if A > B (i.e. the answer is positive) involves either discarding the extra digit (10's and 2's complement) or discarding the extra digit and adding 1 (9's and 1's complement) and if A < B (i.e. the answer is negative) we can leave the value as it is if we want to store it or if we want to print it we just take the negative of the complement.

So which is better for binary? 1's complement or 2's complement?

Why to go with 1's and not 2's:

• getting the complement is easier with 1's complement because you just invert each bit
• 1's is symmetric i.e. 4 bits goes from -15 to 15 but 2's is assymetric

Why to go with 2's and not 1's:

• 2's can be implemented with two rules: get the 1's complement and add 1 or search from right to left until you find a 1 and after that you start inverting
• when subtracting with 2's complement you can just discard the end-carry whereas with 1's you need to discard it and add 1
• 1's complement has two zeros which is very bad considering how often computers compare values to zero
• whether the number is positive or negative, if a number in 2's complement is even, then the rightmost big is 0 which is good for testing whether an integer is even (in 1's complement that bit is 0 for negative odd numbers)

Seems pretty compelling to me to choose 2's complement, which is why it's the most commonly used system for representing integers in binary.

What's Up With MST Fast Implementations?!

In the last post we looked at Prim's and Kruskal's Algorithms and proved that they were correct i.e. that they produced minimum spanning trees (MSTs). In this post we'll look at their running times and consider if there are ways to speed them up (spoiler alert: there is, and it's beautiful).

Prim's:

In order to know how to go faster than our current implementation of Prim's Algorithm, we need to know how fast our implementation is! Let's look at the pseudocode again (this time using the set notation where V is the set of vertices, X is the set of vertices in our MST so far, V-X is the set of vertices not in the MST yet, and T is the set of edges in our MST so far)

1 Pick some vertex and add it to X
2 While not all vertices are in X:
3     If there is an edge crossing the cut (X,V-X) of minimum cost:
4         Add the edge to T
5         Move its incident vertex in V-X from V-X to X
6 return the graph (X,T)
     
What would be the asymptotic running time of this algorithm?

at line 1 we just need to pick some vertex so that can be done in constant, O(1), time. As for the while loop, you're going to be adding n-1 vertices to X because there are n vertices and you added the first in step 1, meaning there are O(n-1) = O(n) loops. For each loop you need to go work out whether an edge is crossing the cut, meaning you need to look at each edge and determine if one endpoint is in X and the other is in V-X (the vertices could store their set as a boolean value). This means we'll need to scan all m edges with each loop, giving us O(m) time for each loop (lines 4,5 are both constant time so we don't need to worry about those). So with O(n) loops each with O(m) time complexity we have an overall time complexity of O(nm).

Considering that m >=  n - 1 (as shown in the previous post on MSTs) our best case scenario is O(n^2), which is reason enough to ask 'can we do better?'

So with each loop we're looking for the minimum edge crossing the cut, and a data structure whose life is all about repeated minimum computations is the heap. Recall from the post on heaps that heaps can have nodes inserted and deleted in logarithmic time, and also perform the extract-min operation in logarithmic time. Also, building the heap from scratch can be done in linear time (if you do it right).

A good idea would be to give each edge a node in the heap so that the root is always the cheapest edge. This is good for looking at the cheapest edges first but the odds of the graph's cheapest edge crossing the cut (X,V-X) at some point in the algorithm is fairly low. A better idea is to use vertices, with the key of each node corresponding to the vertex's edge cost for its edge crossing the cut (meaning if it doesn't have an edge crossing the cut it's key will be set to inf.). This means we'll be changing the key values of the nodes a lot which will require a lot more reassembly of the heap than if we used edges, but it also means that the root of the heap will always give you the vertex you want to add to X (and the corresponding edge) meaning you can just perform a series of extract-mins and you'll end up with the MST.

So with our heap we want to maintain two invariants:
1) the elements of the heap are vertices in V-X
2) for v in V-X, key[v] = cheapest edge (u,v) with u in X, where if no such edge exists, key[v] = inf.

What's the time complexity of building this heap in the first place? Well first you need to find out what the key of each vertex is, which requires you to check every edge once. You go from edge to edge asking 'is this edge crossing the cut?' and if so, if the edge cost is lower than the incident vertex's current key then the vertex's key becomes the cost of the edge. So that's O(m) time. The next step is simply building the heap using the keys which can be done in linear time so we end up with a total of O(m+n) speed.

So if we just went and did n extract-mins to make our spanning tree, that would be O(nlogn) time, but we need to do more than that because after extracting a vertex, and putting it in X, the cut changes and vertices which previously had a key of inf. i.e. no edge crossing the cut, may now need to have their key re-evaluated. Luckily the only vertices we ever need to consider after adding a vertex v to X are the ones incident to v which are in V-X (we'll call such a vertex w), as their edges are going to end up crossing the cut. For a vertex w we simply delete their corresponding key from the heap (this will require us to keep track of where a vertex's key is on a heap, which can just be stored with the vertex itself) then recompute w's key i.e. the cost of the cheapest edge incident to w which crosses the cut, then we insert w's new key back into the heap.

How many times will we be doing this? Each edge can only be responsible for at most one delete-insert combo, as one of its incident vertices will get sucked into X and then with the incident vertex still in V-X we just see whether this edge cost is lower than the vertex's current key and if so, we delete the vertex's key, assign the edge cost to the vertex's key and re-insert it. As deletions and insertions both take O(logn) time and we can have at most m of these operations, we'll end up with O(m*2logn) = O(mlogn) time in terms of maintaining invariant #2 across the life of the algorithm.

To recap:
1) initialising the keys and building the heap costs O(m+n)
2) extract-mins cost O(logn) and there are n-1 of them to do giving us O(nlogn) for that
3) maintaining invariant #2 costs O(mlogn) time

So our total time complexity is O(m + n + nlogn + mlogn) and as m >= n-1 we can always use m as an upperbound for n meaning our mlogn term is the 'strongest', leaving us with a final time complexity of O(mlogn), which is far better than the naive implementation running time of O(mn).

Moving onto Kruskal's:

What's the time complexity of the naive implementation of Kruskal's? Well considering that we go through each edge from cheapest to most expensive, we must first sort them by cost, which can be done via a quicksort in O(mlogm) time. As for each iteration of the algorithm's while loop, if the edge doesn't produce a cycle then we add it, and the definition of a cycle is where you've got two paths between u and v which don't share any edges. If placing an edge which is incident to u and v produces a cycle, then there must already be a path between u and v. In order to see whether such a path exists we can just do a simple graph search in linear time (I'll leave the implentation of that to another post), and considering we may consider every edge at some point then our time complexity for this is O(mn). That leaves a total running time of O(mlogm + mn) and working out which is the strongest term is half-simple: m is bounded by n^2 because if you consider the adjacency matrix you can have a max of n(n+1)/2 edges. You can therefore replace logm with log(n^2) which is 2logn and as they differ by a constant they are interchangeable, so our running time ends up being O(mlogn + mn) and obviously n is stronger than logn so our strongest term is the mn thus we're left with O(mn).

What would really speed this algorithm up would be a data structure that let us remember whether two nodes have a path between eachother i.e. they're in the same cluster. How about we make a data structure called a union-find which works like this: each cluster has a 'leader' vertex which acts as an identifier for that cluster, and all vertices store the index of their cluster's leader (or SOMETHING to identify it). This means that to check whether two vertices are in the same cluster we can just ask whether two vertices have the same leader, meaning this step can be done in constant time. This is called the 'Find' operation so it's no surprise that the second operation of this data structure is the 'Union' operation. This is where you get two clusters and fuse them together, which is what happens in Kruskal's when you add an edge that bridges two clusters together. If we perform the union operation on clusters A and B where A has fewer vertices (we can store the size of the clusters in a hash table or something), then we'd want to set the leader of all the vertices in A to the leader of B, because it will require less changes. Now we need to ask how many times can this happen in a single run of the algorithm?

Let's consider a single vertex v. Say in the first iteration it's lucky enough to form a cluster with another vertex u which is incident to the first edge added to the MST. Because each vertex started off as its own leader (as they were in clusters of size 1) now we just randomly choose which one becomes the new leader, and maybe that leader is u, so v switches its leader to u (meaning 1 switch so far). We're trying to find the worst case scenario for our vertex in terms of number of switches so if the next edge just connects another vertex to our cluster of two, v's leader won't change because it belongs to the larger cluster. But if instead the second edge gets added to a completely different place, forming another cluster of two, and then those two clusters need to be combined in the next iteration, then worst case says our vertex v will need to swtich its leader again (2 switches now). Notice that each switch means the cluster has at least doubled in size, and starting a cluster of size 1, the cluster can only double in size log2(n) times, meaning worst case scenario is that a vertex switches its leader O(logn) times. Considering there are n vertices this means we'll never have anymore than O(nlogn) switches.

So combining our initial sorting O(mlogm) and our cycle-checks (which includes the total O(nlogn) leader swtiches and finding whether two vertices are in the same cluster which is O(1) and happens O(m) times) we end up with a time complexity of O(mlogm + nlogn + m) where the strongest term is mlogm so we end up with O(mlogm) timecomplexity, meaning now our bottleneck is the sorting that occurs at the beginning of the algorithm.

This is the same running time we got with the speedy version of Prim's as O(mlogm) and O(mlogn) are, as explained above, interchangeable.

NOT BAD. So not-bad infact that I had a tear in my eye when I found out why the faster implementation of Prim's Algorithm with the O(mlogn) factor worked, and similarly the way that the union-find data structure for Kruskal's gives each vertex a max of log2(n) leader changes is awesome.

Sorry I couldn't snaz this up with pictures, but I have a lot to get through in a very short period of time. Next up will be the storage of signed integers, and maybe some stuff on floating point values, then I'll dive headfirst (with little regard for my mental health) into evolutionary dynamics.

What's Up With Number Bases?

Humans evolved to have 10 fingers, so it's no surprise that the arithmetic which surrounds our day-to-day life uses numbers that are to base 10. What does this mean? In representing numbers, we really have two options. The first is to have a single symbol to represent every number, for example you could go 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F,G,H,I,G,J,K,L,M,N,O,P... and after you're out of english letters you can use greek, then chinese and eventually elaborate paintings of assortments of fruit as you count higher and higher. The second option is to use a limited set of symbols which carry extra meaning when placed alongside eachother into digits. Base 10 uses 10 symbols: 0,1,2,3,4,5,6,7,8 and 9. You could decide that each digit holds the same weight i.e. 139 could mean 1+3+9, but we would obtain the same number using 1+4+8 i.e. 148, meaning testing for equality wouldn't be easy, not to mention large numbers would require many many digits. However we can solve both these problems by just saying the first digit in a number (starting from the right) represents its [symbol's value] * [the base]^ 0, and then say the second digit represents the [symbol's value] * [the base]^ 1 and so on, and the whole number is all of these things added up. In base ten this means that the number 139 is actually:

9 * 10^0 = 9 * 1 = 9
+
3 * 10^1 = 3 * 10 = 30
+
1 * 10^2 = 1 * 100 = 100
=
100 + 30 + 9

The reason that this setup can allow for each integer to be represented is that each digit to the left of the core digit (I made that term up but I'm sure you can intuit that I'm referring to the 9 in the above example) can be expressed as just a heap of 'ones'. Consider the number 39:

There's certainly nothing special about using a base of 10 as opposed to another other base. All the above rules apply to something like base 8 (octal numbers). Base 8 uses the symbols 0,1,2,3,4,5,6 and 7. If you're working with base 8 and you see the number 139 it means 9 * 8^0 + 3 * 8^1 + 1 * 8^2 = (in base 10) 9 + 24 + 64 = 97. Just like with base 10, base 8 can represent every integer and each integer has a unique representation which is pretty cool in my opinion. We could have evolved to have 8 fingers rather than 10 and all the little tricks we learn from multiplication like 'when timesing by 5 just halve the number and add a 0 digit' would be gone and we'd have other tricks to easily work our way around arithmetic using the base.

You may wonder 'why would we ever need to worry about bases other than 10 if it's obvious that we can do everything we need to using the base'? The answer is that computers can only represent data in the form of bits (1s and 0s) meaning that if you want to store the number 139 (in base 10) in a computer you'll need to find a way to convert it into 1's and 0's. Well how about a base which has two symbols, 0 and 1, called 'binary'. A lot of this post will be about converting between the two.

First off let's visualise what's going on with different bases of numbers. The following picture shows what is looks like when a heap of bases represent the number that base 10 calls 39. On the left of each level is the size of that level's 'chunks' i.e. what one chunk represents in terms of ones. The numbers on the right hand side of each level are the symbols that represent the number of chunks in the level. Reading top-down through the symbols, you get the number that the base spits out when you ask it what its representation of 39 is. For base infinity i.e. the base with only a single digit, I just made some crazy looking symbol.

As you can see, the bottom level of base 4 is never going to have 4 chunks because that can be represented by a single chunk in the level above it, meaning it can only ever have a max of 3 chunks. The same can be said for the second (purple) level; it can only have a max of 3 chunks because if it has 4, that can be represented by a single chunk in the green level. Not only 'can' it be represented like that, but it must be, as base 4 only had 4 symbols: 0, 1, 2 and 3, meaning you cannot have 4 chunks on one level and if you do, you just give it to the level above.

let's look at how you could construct these numbers if you just started with the row of ones from base infinity. We'll do base 3 first: you know you can't represent all 39 of the chunks on the bottom row because your max symbol is 2 so you tell all of the chunks on the bottom row to find two friends and form a chunk on the above row. Luckily for us there aren't any leftovers so we can just go to the next row and see if we've got few enough chunks this time. So we look at the purple row and we have 13 chunks which is still too much meaning we ask the chunks to form groups of 3 and jump to the next row. In this case we have 1 leftover (remainder) who didn't have the social skills to get in early with the grouping, so he gets left on that level (no problem for us though because there's 1 chunk and we can use the symbol '1' to represent that). So we had 13 chunks and divided it into 3 groups and ended up with 1 remainder, so we've got 4 groups on the green level. Again, it's too much so we get them to form groups of 3 again, and again 1 gets left behind. We go up to the cyan level and because we have a number of chunks (1) that we have a symbol for, we can stop there (in fact we wouldn't be able to go up another level if we wanted to because 1 chunk on the above level represents 3^4 = 81 ones which we clearly don't have on the cyan level).

So we end up with the number 1110 in base 3, with each '1' representing the chunks that didn't go on to the next level. We know each chunk contains 3 times as many ones as a chunk in the next level down and that in the bottom level 1 chunk = 1 one so going right to left we can count in base 10 to see we have
0 * 1 + 1*3 + 1*9 + 1*27 = 3 + 9 + 27 = 39
which is what we started with, meaning our method works.

So what exactly was our method? We start off with no digits and a string of ones (which we talk about as 39 in base 10 terms because we're so familiar with it) and we add a digit which is the remainder when we divide the 39 by our base (in this case 3), and then we actually divide the 39 by 3 and continue the process with the quotient (the non-remainder part of the division), until the result of dividing is 0 (because that's the point when there are no more chunks which can group up and go to the next level).

If we were to make an algorithm for this, starting with the number n and using base b it would look like this:

Convert_From_Base_Ten(n,b):
    number <-- ""
    while n != 0:
        number <-- str(n % b) + number
        n <-- n/b
    return number

Above we did the reverse process where you take each digit and multiply it by its associated value, and then sum them all up e.g. 0 * 1 + 1*3 + 1*9 + 1*27 = 3 + 9 + 27 = 39. Let's see how the algorithm would look for that:

Convert_To_Base_Ten(number,b):
    n <-- 0
    for i in xrange(0,len(number)):
        n <-- n + number[i] * b^(len(number)-1-i)
    return n

So we've taken care of integer conversions, BUT unfortunately we've left out one whole half of the digits: the ones one right of the decimal point. Just as the core digit represents your base to the power of 0's and digits to the left have ascending powers, digits to the right i.e. the fractional digits have descending powers. the number 0.325 in base 10 is 3*10^-1 + 3*10^-2 + 3*10^-3. Likewise the number 0.101 in base 2 is 1*2^-1 + 0*2^-2 + 1*2^-3 = (in base 10) 0.5 + 0.125 = 0.625. This calculation should be evidence enough that going from any base to base 10 isn't difficult, but the same cannot be said for the reverse process.

To understand the process of going from base 10 to some other base, we must first realise that the digital number system lets us shift digits left or right by multiplying or dividing by the base. For example 104 in base ten becomes 1040 if you multiply by ten or 10.4 if you divide. If you consider the visualisation above, when you multiply a number by its base you're going to each level and giving each chunk (base - 1) friends which is precisely enough to jump up to the next level so everything gets shifted up one level, and the reverse is true for division.

I'll focus on binary because that's really the one big base that we care about: If you want to know what the fractional digits of a binary number are but you can only see the core digit, you can just multiply the number by 2 and write down the digit that shows up in the core digit, then repeat that process until you're left with just 0's coming in or some repeating sequence of digits. BEAR WITH ME. Alright so say you wanted find out the binary equivalent of the number 0.582 in decimal. You can follow the exact same process: just times by 2 and you'll get 1.164. The thing here is that the core digit doesn't lie i.e. it means the same thing regardless of what base you're talking about, meaning that 1 would have showed up if you started with 0.582 in binary, so you just follow the process and write it down. Now I would say times 1.164 by two but the problem here is that the first '1' isn't going anywhere; in binary it would be shifted to the right and gotten out of our way by another multiplication by 2. Considering that's not going to happen here we'll just need to manually get it out of our way by subtracting it off. So once we're left with 0.164 we can multiply by 2 again, giving us 0.328. We write down the digit (0) which means we now have '10' written down corresponding to 0.10 in binary. repeat the process; now we have 0.656, so write down another 0. After a while I ended up with 0.100101010111 which didn't look like it planned on terminating any time soon.

So that's our process for going from decimal to binary. Note that this works with all non-decimal numbers; however if you want to use something like hexadecimal (base 16) then you'll need to consider the two digits to the left of the decimal point rather than just the 1st (because if you times say 0.9 by sixteen the number you're left with overflows the core digit). Remember what I said above: the core digit is the only one which doesn't lie, so if you're dealing with hexadecimal you'll need to do a conversion from the decimal to hexadecimal i.e. a conversion within a conversion. Luckily this isn't difficult because you can just look at the first two digits and go straight to the hexadecimal equivalent i.e. 01 --> 1, 02 --> ... 10 --> A, 11 --> B ... 15 --> F. I would give an example but you would be surprised how hard it is to find a fractional number in base 10 which doesn't give a recurring sequences in base 16.

The general algorithm for converting a fractional number n from base 10 to base b is:

Convert_Fractional(n,b):
while n!=0 and (there aren't any repeating digit patterns):
    i <-- -1
    n <-- n * b
    number <-- number + Convert_To_Base_Ten(<digits to the left of the decimal point>,b)*(b^i)
    i <-- i - 1
    n <-- n - <digits to the left of the decimal point>

Anyway so we know how to convert to and from base 10 in terms of both integer and fractional parts. But in truth we can convert between numbers of any two bases because our algorithms just happened to be thinking in terms of base 10 when you could be thinking in terms of any base.

Now going straight from binary to decimal and back is pretty laborious because it takes a lot of steps, but going from hexadecimal to decimal and back is very easy (far fewer digits) meaning it would be very convenient if converting between binary and hexadecimal was easy because it would allow us to use hexadecimal as a middleman between the two bases. Let's see if it is:

four binary digits can cover the same range of numbers as a single hexadecimal digit:

0000 = 0    0001 = 1    0010 = 2    0011 = 3
0100 = 4    0101 = 5    0110 = 6    0111 = 7
1000 = 8    1001 = 9    1010 = A   1011 = B
1100 = C   1101 = D   1110 = E    1111 = F

meaning the number 1101 1010 0101 . 0100 0011 1111 is the same as DA5.43F. We could have used the conventional techniques to work that out but obviously the ability to group the digits up into sequences of 4 and convert each one makes our job a lot easier. The story is similar with binary and base 8; except there are three binary digits to each octal digit. It works because the bases are all the same number to a different power. With hexadecimal, each digit (2^4 symbols) encapsulates the information of 4 binary digits (4 digits of 2^1 symbols each giving 2^4 total permutations).

So we know that going from converting between binary and hexadecimal is trivial, and we know converting between hexadecimal and decimal is easier than converting between binary and decimal, so it's clear that converting between binary and decimal is best done with the hexadecimal middle-man.

So far example we can use the number from above: 1101 1010 0101 . 0100 0011 1111 as an example. We get to the hexadecimal number DA5.43F and then from there we want to be decimal so we first look at the DA5 part:

5 * 16^0 + 10 * 16^1 + 13 * 16^2 = 160 + 832 = 3493

 Looking at the 43F part :

4 * 16^-1 + 3 * 16^-2 + 15 * 16^-3 = 1/4 + 3/64 +15/1024 = 0.26538085937 in decimal.

So our final answer is 3493.26538085937. Very cool. Going back the other way we can start with 3493.26538 and try to get to hexadecimal:

3493 % 16 = 5

3493 / 16 = 218

218  % 16 = 10 = A

218 / 16 = 13

13 % 16 = 13 = D

13 / 16 = 0

so we get DA5 (good thing too because it's what we started with)

now for the fractional part:

0.26538 * 16 = [4].24608

0.24608 * 16 = [3].93728

0.93728 * 16 = [14].99648 = [E].99658

We can stop there if we think we're accurate enough (the fact that we truncated the value earlier means any further digit calculations wouldn't be very representative anyway). We ended up with 43E which isn't too far off the 43F that we started with; obviously the cause of this was also the truncation above. But nonetheless we're left with DA5.43E. Next step is getting this into binary: which digit for digit is just:

1101 1010 0101 . 0100 0011 1110

Not too bad! Well making this post has done wonders for my intuition on the subject and hopefully you can say the same. Next up I'll hopefully get around to posting about ways to speed up Prim's and Kruskal's Algorithms.

What's Up With Minimum Spanning Trees?!

If you take a graph and select certain edges to form a tree which includes all of the graph's vertices, you've got a spanning tree. If this tree, when compared to all the possible spanning trees you can make from the graph, has the minimum weight, then you've got a minimum spanning tree (MST). We're going to talk about two methods for going from a graph to its MST: Prim's Algorithm and Kruskal's Algorithm. For simplicity we'll consider trees where each edge weight is unique, meaning for any graph there is only one MST.

Prim's Algorithm:
This was the algorithm used by AT&T and other notable telecommunications companies for years, as telecommunication companies often need to find the shortest path for transferring information from one point to another. The algorithm goes vertex by vertex.

We'll start at vertex A (the one you choose is arbitrary because it will end up in the MST no matter what). We then add the adjacent vertex with the lowest edge weight (in this case B) and the edge itself.

So now we've got two vertices and we can choose the next vertex from either. The next smallest weight is connecting A or B to an adjacent vertex is 2 so we can add that edge and K to our MST.

Here's a good time to acknowledge why we don't just add all the adjacent edges from our initial vertex e.g. the one linking A and K: Because the edge we end up choosing (the one linking A and B in that case) will be lower in weight than all other adjacent edges to the initial vertex. This means it's possible to add K to the MST without needing to use the edge of weight 4, and we can find a cheaper way. But then you might ask when we added the edge of weight 2 to the MST, how do we know it's not cheaper to link K and J with the edge of weight 1 rather than use the edge of weight 2? The answer is that from B we chose the cheapest edge, meaning to get to K through J we know it would be a longer path than just going from B to K, and if the edge of weight 1 is going to be added to the MST it'll be via our vertex K rather than the other way around, meaning we don't need to add the comparatively expensive edge of weight 5 connecting B and J.

Speaking of which the next cheapest edge connecting to an unvisited adjacent vertex is edge {K,J} so we add that and J. Then we can add H and {J,H}, then C and {B,C}, then D and {C,D}.

Looking at I, we have two choices: 10 or 13. Obviously we're going to pick 10 because it's lower so we can add I and {D,I}. A trend we're seeing here is that Prim's Algorithm always makes the best decision even if you're just looking locally. This makes it a greedy algorithm and as the problem has optimal substructure (i.e. you'll the optimal solution to a local problem will be optimal in terms of the whole problem) this is very convenient. Notice that if we had started the MST with I, we would have chosen the edge 10 as well and we would have made our way around the graph until J had been added, but at no point would the edge 13 be added as the method of choosing the cheapest edges would take us from D to C to B to K to J (with a side-stop at A along the way).

So now all we have left to worry about is E and F. Forgetting about the algorithm for a second, we know we can finish this tree by adding any two of the edges 9, 11, and 12 (throughout this post I'll refer to edges by either their weight or their two adjacent vertices). As we want an a minimum spanning tree it makes sense to choose the two with the lowest weights as this ensures the minimum part of the spanning tree is retained. Because we have access to the edges 11 and 12 in the algorithm (due to them being adjacent to D and H which are already in the MST) we add the cheapest which is 11, and then we can add edge 9 meaning our algorithm has given us the two smallest edges naturally. You might be thinking that it was lucky both D and H were part of the MST already so we didn't get stuck with edge 12 e.g. if D wasn't already in the MST but just like above, if this was the case, starting from H and picking all the cheapest edges will naturally form the partial MST above, with D in the MST, meaning under no circumstances would the edge 12 ever be added.

So there's our final MST. Note that it is indeed a tree and that also note how poorly that green colour stands out against the white background. Oh well, I blame Paint for its limited colour palette.

So here's the general algorithm in words:

Pick some vertex and add it to the MST
While not all vertices are in the MST:
    Add the unvisited vertex of minimum distance to the MST and the corresponding edge
return the MST

Too easy.

Now let's look at Kruskal's Algorithm:

With Prim's Algorithm, we started a tree and grew it, adding the optimal edge with each iteration which didn't connect two vertices already in the tree (i.e. we ensured never to make a cycle). With Kruskal's Algorithm, we create a forest i.e. several trees which all grow and eventually merge together to make the MST. Instead of looking for the next cheapest edge adjacent to our partial MST, we simply go for the cheapest edge regardless of where it is in the graph, and this obviously can create more than one tree at the initial stages of the algorithm. Just like in Prim's algorithm, it is important to not make any cycles (as then it wouldn't be a tree). But unlike Prim's algorithm it's not as easy to know whether you'll be making a cycle because in Prim's you could just check whether the two vertices incident to the edge where already both in the MST and if so adding an edge would be redundant. In Kruskal's Algorithm you may need to link two forests together meaning you'll need to link two vertices already in the MST which means you'll need a means of knowing whether they're in the same cluster or not.

Starting with the same graph, our smallest edge is 1, connecting J and K. Obviously adding this edge won't make a cycle so we add the edge and the two vertices to the MST.

Now we go to the next smallest edge: 2. Adding this won't make a cycle so we do it. Then we can add 3, but we can't add 4 because it will make a cycle. We can't add 5 either for the same reason, so we continue on to 6 which we can add.

Next cheapest edge is 7 so we've finally gotten to a new cluster. The next is 8 and here we have an interaction between our two clusters. Although it's visible to us that no cycles are going to be made by adding the edge, the algorithmic approach would be to check all of C's neighbours and those neighbours' neighbours and so on until you know all of the vertices in that cluster, and if B isn't in that cluster it's okay to add the edge. There are two parts to kruskal's algorithms: creating/expanding a tree and linking two trees. The creating/expanding part's correctness is provable by analogy to Prim's Algorithm: If the next cheapest edge is coincidentally going to be appended to an already existing cluster then Prim's Algorithm would have added that edge anyway because it chooses the locally cheapest edge and if there is a globally cheapest edge which is local then it will also be the locally cheapest edge. As for the linking part, two clusters must be linked one way or another and Kruskal's Algorithm always opts for the next cheapest edge meaning it's impossible for there to be a cheaper way of linking two clusters, because if there was a cheaper path to link two clusters then the individual edges along that path would all need to be cheaper than the edge in question in which case they would have already been considered by the algorithm.

Next up we add 9 so now again we have two clusters in our forest. then we go to 10 which gets added, then 11 for which we link the two clusters into one as we know no cycles can be made. We then go to 12 which would produce a cycle because F and H are now in the same cluster, so we ignore 12. Finally we look at 13 which also will create a cycle if added, as J and I are already in the cluster. Our algorithm wouldn't even need to consider these last two steps if we tell it to stop as soon as all the vertices are in the MST which they are by the time we've added 11.

There you have it, we've ended up with the exact same MST that we did with Prim's Algorithm. Here's the pseudocode for Kruskal's Algorithm:

While not all vertices are in the MST:
    if the cheapest edge not in the MST will not produce a cycle via its addition:
        add the edge to the MST
return the MST

I've given some wordy explanations of why certain things work about these algorithms but here I want to get into more of a formal approach to proving that both of these algorithms indeed are 'correct' i.e. they do indeed produce minimum spanning trees.

I'll start by defining a 'cut'. Recalling that the set of vertices in our graph is V, a cut is a partition of V into two non-empty sets, meaning you decide for each vertex whether it's in group A or B, and you call the cut (A,B). You can refer to the cut as the boundary between the two groups or the two groups themselves; whatever suits your needs. Each edge will either be linking two vertices in A, two vertices in B or a vertex from each group. The edges which interact with both groups are said to 'cross the cut'.

How many cuts can you get out of a graph with n vertices? Well we can go to each vertex and decide whether it's in group A or B. Because there's two possibilities with each vertex we'll end up with 2*2*2*2... n times or 2^n. But we need to consider the condition that both sets cannot be empty meaning the possibility that all vertices are in A and the possibility that they're all in B must be subtracted, leaving us with 2^n - 2 possible cuts.

We'll do Prim's Algorithm first and before we prove that it produces a minimum spanning tree we must prove that it produces a spanning tree.

We'll start with  the simple lemma (a lemma is a stepping stone towards a proof) that if a graph is disconnected, you can make a cut which has no edges crossing it, and vice versa. By definition a graph is connected if there is a path from every vertex to every other vertex. This is called the empty-cut lemma.

We can select two vertices u and v, and assuming there is no path from u to v (the graph is disconnected), it's easy to show that you can make a cut between the two vertices and have no edges crossing it (i.e. an empty cut), by defining A as all reachable vertices from u and B as all reachable vertices from v and then acknowledging you've got two non-empty sets (a cut) for which no edges cross. Going the other way, we can assume there is a cut between u and v for which no edges cross and it's clear that there cannot be a path from u to v because such a path requires an edge to cross the cut. I am aware of how blatantly obvious this lemma is but we must play by the mathematical proof-making rules if we are to create a rigorous proof.

So now we've got a way of talking about connectedness in terms of whether you can make an empty cut from the graph.

Second lemma: the double crossing lemma:

This one states that if you have a cut and you have a cycle which includes vertices in A and B, then there must be more than one edge crossing the cut participating in that cycle. The reason is that a cycle is a path that begins and ends at the same vertex, without re-using edges. This means that if your cycle begins in A and goes to B, it must come back via another edge and vice versa if you consider it to start in B. This lemma is actually a weaker version of saying that there will be an even number of edges crossing the cut because each time you cross the cut, you need to cross back again.

This leads us to the Lonely Cut Corollary (a corollary is a proposition which follows from something already proven), which states that if there is only one edge crossing a cut, it is not part of a cycle.

Alright so we've set up the two basic lemmas that we need, now let's consider a bit of terminology. The set of vertices which our algorithm has added to the MST is X and the set of edges is T. This means the vertices not yet added are in the set V-X. If a set of edges 'spans' a set of vertices then the graph produced from the edges and vertices is connected (no empty cuts).

1) T always spans X. This is because the algorithm always adds one vertex at a time and when it does, it connects that vertex to the MST via an edge, so considering the algorithm never leaves the MST to go and start a new tree (like in Kruskal's Algorithm), we'll always have a connected graph.

2) When the algorithm's done, X = V. This is because for us to not have all the vertices in X by the end, then at some point we'd have an empty cut (X,V-X) and if that's the case then our graph is disconnected and we only take connected graphs as input. Combining 1 and 2 tells us that by the end we'll have a connected graph containing all the vertices.

3) No cycles ever get created in T. This is because at each point in the algorithm you're adding an edge that crosses the cut (X,V-X) and in doing so, you grow X by one vertex and shrink V-X by one vertex. This means that next time you're going to be doing exactly the same thing with the new cut (X,V-X). As we stated in the double-cross lemma, a cycle requires two edges crossing the same cut so in order to create a cycle you would need to add the edge to your MST without changing the two vertex sets; thus we always get a lonely cut and never create a cycle.

Pictorially let's look at why cycles don't get made:

Recalling that Prim's Algorithm only considers edges which cross the cut, let's say that the edge to j is the next cheapest one.

So now we have two possible edges leading to k. If we were to add both we'd get a cycle. Because the choice is arbitrary, let's say the edge from j to k is the cheapest:

And now the edge that went from i to k is black. Why? Because X expanded to include k meaning that the edge no longer crosses the cut and thus will never be considered again by the algorithm, so the cycle cannot be made. The same can be said for all edges which could complete a cycle: you need two edges across the cut to make a cycle and with each iteration the algorithm will choose one edge and expand X, forgetting about previous candidate edges which once crossed the cut to the same vertex.

So there's our long-winded proof that Prim's Algorithm indeed makes a spanning tree. Speaking of trees this reminds me of the scene in Lord of the Rings where Treebeard tells the two hobbits after a very long discussion with fellow trees (okay they're actually 'ents' for the lotr fans) that they've all decided the hobbits aren't orcs. Nonetheless let's power on to finding out why the algorithm gives us a minimum spanning tree.

So the first thing we need to do is prove the 'cut property' which states that if you have a cut (A,B) and of the edges crossing it, e is the cheapest, then e will be in the MST. We'll do this by contradiction: assuming we have an optimal solution, then exchanging an edge for e to get a better solution, which contradicts the assumption that our original solution was optimal.

So let's say in the MST which we'll call T* we have a cut (A,B) and although e is the cheapest edge crossing that cut, we instead have f in T*, which is more expensive. Obviously we need some edge or otherwise we'd end up with a disconnected output which wouldn't be a spanning tree (based on the empty cut lemma).

It would be easy here to make the exchange argument that we can just swap f and e and get a spanning tree with a lower weight than T* thus contradicting the assumption that it was the MST in the first place. However the double-edge lemma tells us that it's possible to create a cycle in doing so: because it's possible that g is an edge also in T* and you can imagine that carelessly exchanging f for e can allow for a cycle to be made which wasn't present before.

Not only this, but if we exchanged f for e we'd leave a vertex disconnected in B. This tells us that we can't just swap any two edges and hope to be left with a MST. Having said that, it is always possible to exchange e with some edge, which in this case is g. If we took g out and put e in, meaning we'd have e and f crossing the cut, we wouldn't have any cycles or disconnects and as e is the cheapest edge crossing the cut we would have reduced the total weight, thus contradicting the assumption that T* was an MST.

But how do we know that if T* is not an MST, there is an edge g that can be exchanged with e in some cut to give a lower weight spanning tree without any cycles or disconnects?

Observe that when you have a spanning tree, adding any extra edge will produce a cycle because if the endpoints of the added edge are u and v, then as they already had a path from one to the other (which is part of the definition of a tree: each vertex has a path to every other vertex) the new path given by the edge will produce a cycle (as two separate paths from u to v create a cycle). So if we add e to our spanning tree, we know a cycle will be made. Using the double edge lemma we know that a cycle which crosses a cut at least once must cut it twice, meaning there will be another edge (in this case g) which we can remove to break the cycle. In doing so we will certainly reduce the total weight of the spanning tree because we knew at the beginning that e was the cheapest edge crossing the cut.

Now we need to consider the chance of any disconnects after exchanging the two edges. Because the vertices in the cycle had two paths between them, after removing g and thus breaking the cycle, there will still be one path between them, meaning we don't lose any connectivity in the spanning tree.

So if we have a T* for which such an exchange is possible, then T* is not a minimum spanning tree, and if no such exchanges are possible, it is a minimum spanning tree. This gives us the cut property where for any cut in a graph, the cheapest crossing edge will be included in the MST. As Prim's Algorithm always chooses the cheapest edge crossing the cut (X,V-X) (where X=A and V-X = B in the above exchange approach) due to utilising the cut property, it will end up without any opportunities for such an exchange meaning that it indeed produces a minimum spanning tree.

Now onto Kruskal's Algorithm. Again we need to prove it indeed produces a spanning tree i.e. it has no cycles and no disconnects. Again, we'll say T is the set of edges produced by the algorithm at any point in that algorithm's runtime.

The cycles part of this proof is easy because Kruskal's algorithm specifically prohibits the adding of any edges which will produce a cycle, so this is self-evident.

The connectedness part is a little bit more tricky. We can use the definition of connectedness that for any cut (A,B) in our graph G, there must be an edge crossing it in the MST. Assuming Kruskal's Algorithm considers all edges at one point, and that our input graph G was connected (and thus has at least one edge across every cut) all we need to say is that via the lonely cut corollary the algorithm will have no problem adding an edge across any given cut to T when previously there were no such edges in T because doing so won't create a cycle, as a cycle which crosses a cut requires two edges to cross it. So as each cut in our output will have at least one edge crossing it, we know the output is connected.

This is assuming we consider each edge which isn't true, as we can stop as soon as we have added all the vertices. We'll know we've added all the n vertices when we've added n - 1 edges. Why? Consider a tree and you pick a random vertex. Then to reach the other vertices you need one edge each hence you end up with n - 1 edges. If you have n - 1 edges and no cycles (which this algorithm will give you) then you necessarily have a spanning tree.

As for Kruskal's Algorithm producing a minimum spanning tree, it's not as simple as it was with Prim's. With Prim's the pseudocode explicitly appeals to the cut property where you add the cheapest edge crossing the cut (X,V-X), but here the algorithm is just adding the cheapest edge which doesn't create a cycle. We need to show that the algorithm inadvertently appeals to the cut property.

So let's say we're going to add an edge e which links u and v. Obviously u and v will be in different clusters or otherwise there would already be a path between them and by adding the edge we'd be producing a new path and hence a cycle. This means we can manufacture a cut between the two clusters for which our edge crosses. As for the other clusters, whether they're in A or B is irrelevant. The fact that the algorithm is considering e before any of the grey edges means that it is the cheapest. The fact that e is the cheapest edge not yet added to T means it must be the cheapest edge crossing the cut and by the cut property, the cheapest edge across any cut belongs in the MST. The only reason the Kruskal's Algorithm has to not include the edge is if it creates a cycle which is impossible because the cut was empty at the beginning of the current iteration of the algorithm and adding an edge across it cannot possibly form a cycle by the lonely cut corollary.

So we know that Kruskal's Algorithm doesn't produce any cycles and doesn't output a graph with disconnects, and satisfies the cut property, meaning it indeed produces a minimum spanning tree.

I'll leave the post there because it's gotten quite long, and next post I'll talk about faster implementation methods such as heaps in Prim's Algorithm and the Union-Find data structure in Kruskal's Algorithm.

Special thanks to the youtube channel YogiBearian for great explanations on minimum spanning trees.